Republic of Pwning

En el Main CTF de la Ekoparty, desde hace algunos años, se incluye la categoría Sponsors. Esta categoría agrupa retos propuestos por los auspiciadores de la Ekoparty. En ella se pueden encontrar retos variados y muy originales desde descifrar radioseñales, controlar robots, car hacking, impresión 3D, etc. Particularmente me gustan los retos que propone Onapsis porque son bastante didácticos. Este año el reto de Onapsis se trataba del cifrado AES. En este post quiero explicar como lo resolví y lo aprendido en el proceso. Espero lo disfruten.

Descripción

Une de nuestres researchers implementó AES en python. Con dicha implementación, cifró 2 archivos, uno de testing y el flag. Ambos archivos, encriptados, junto con la implementación, fueron subidas al repositorio de código. Volando de vuelta desde un cliente, perdió su computadora, junto con las versiones sin encriptar de los archivos y la CLAVE utilizada para cifrar los archivos. Necesitamos la flag con urgencia, elle solo recuerda haber probado la implementación encriptando “testingaes123456” y que la flag tenía el formato ONA{}. ¿Nos podés ayudar a recuperar la flag?

Nos entregan 3 archivos: aes.py, cipher.txt y testcipher.txt. El primero es una implementación de AES en Python y los dos siguientes son, respectivamente, el flag y la cadena testingaes123456 cifrados con la misma clave.

Análisis

Lo primero que hice fue revisar el archivo aes.py. Por suerte he pasado algún tiempo en Cryptohack y pude notar rápidamente que la tabla s_box es diferente a una implementación estándar: la del reto está ordenada de forma ascendente. Todo lo demás parecía estar en orden ¿Pero cómo afecta esto al cifrado?

s_box = (
    0x00, 0x01, 0x02, 0x03, 0x04, 0x05, 0x06, 0x07, 0x08, 0x09, 0x0A, 0x0B, 0x0C, 0x0D, 0x0E, 0x0F,
    0x10, 0x11, 0x12, 0x13, 0x14, 0x15, 0x16, 0x17, 0x18, 0x19, 0x1A, 0x1B, 0x1C, 0x1D, 0x1E, 0x1F,
    0x20, 0x21, 0x22, 0x23, 0x24, 0x25, 0x26, 0x27, 0x28, 0x29, 0x2A, 0x2B, 0x2C, 0x2D, 0x2E, 0x2F,
    0x30, 0x31, 0x32, 0x33, 0x34, 0x35, 0x36, 0x37, 0x38, 0x39, 0x3A, 0x3B, 0x3C, 0x3D, 0x3E, 0x3F,
    0x40, 0x41, 0x42, 0x43, 0x44, 0x45, 0x46, 0x47, 0x48, 0x49, 0x4A, 0x4B, 0x4C, 0x4D, 0x4E, 0x4F,
    0x50, 0x51, 0x52, 0x53, 0x54, 0x55, 0x56, 0x57, 0x58, 0x59, 0x5A, 0x5B, 0x5C, 0x5D, 0x5E, 0x5F,
    0x60, 0x61, 0x62, 0x63, 0x64, 0x65, 0x66, 0x67, 0x68, 0x69, 0x6A, 0x6B, 0x6C, 0x6D, 0x6E, 0x6F,
    0x70, 0x71, 0x72, 0x73, 0x74, 0x75, 0x76, 0x77, 0x78, 0x79, 0x7A, 0x7B, 0x7C, 0x7D, 0x7E, 0x7F,
    0x80, 0x81, 0x82, 0x83, 0x84, 0x85, 0x86, 0x87, 0x88, 0x89, 0x8A, 0x8B, 0x8C, 0x8D, 0x8E, 0x8F,
    0x90, 0x91, 0x92, 0x93, 0x94, 0x95, 0x96, 0x97, 0x98, 0x99, 0x9A, 0x9B, 0x9C, 0x9D, 0x9E, 0x9F,
    0xA0, 0xA1, 0xA2, 0xA3, 0xA4, 0xA5, 0xA6, 0xA7, 0xA8, 0xA9, 0xAA, 0xAB, 0xAC, 0xAD, 0xAE, 0xAF,
    0xB0, 0xB1, 0xB2, 0xB3, 0xB4, 0xB5, 0xB6, 0xB7, 0xB8, 0xB9, 0xBA, 0xBB, 0xBC, 0xBD, 0xBE, 0xBF,
    0xC0, 0xC1, 0xC2, 0xC3, 0xC4, 0xC5, 0xC6, 0xC7, 0xC8, 0xC9, 0xCA, 0xCB, 0xCC, 0xCD, 0xCE, 0xCF,
    0xD0, 0xD1, 0xD2, 0xD3, 0xD4, 0xD5, 0xD6, 0xD7, 0xD8, 0xD9, 0xDA, 0xDB, 0xDC, 0xDD, 0xDE, 0xDF,
    0xE0, 0xE1, 0xE2, 0xE3, 0xE4, 0xE5, 0xE6, 0xE7, 0xE8, 0xE9, 0xEA, 0xEB, 0xEC, 0xED, 0xEE, 0xEF,
    0xF0, 0xF1, 0xF2, 0xF3, 0xF4, 0xF5, 0xF6, 0xF7, 0xF8, 0xF9, 0xFA, 0xFB, 0xFC, 0xFD, 0xFE, 0xFF,
)

Resumen de AES

AES cifra bloques de datos de 16 bytes. Primero forma una matriz de $4 \times 4$ bytes con el bloque de texto plano. Esta matriz se llama estado y la reprensentaremos con $S$.

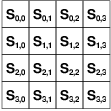
Luego aplica 10 rondas¹ de 4 operaciones sobre el estado: add_round_key, sub_bytes, shift_rows y mix_columns. La única operación que depende de la clave $K$ es add_round_key. Esta consiste en hacer XOR al estado $S$ con la clave de ronda $K_i$². En las demás operaciones no interviene la clave: shift_rows y mix_columns cambian de posición los bytes de $S$ y sub_bytes reemplaza cada byte de $S$ por otro arbitrario. Esta última, es la que nos interesa. Para el reemplazo sub_bytes se fija en la tabla s_box. Así, por ejemplo, el byte 0x23 será reemplazado por s_box[0x23].

La siguiente imagen resume el proceso de cifrado de AES:

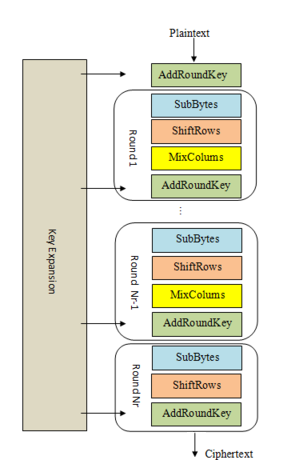Fuente: cryptohack.org

La vulnerabilidad

Quizá ya has notado que al estar la tabla s_box ordenada, los bytes se reemplazan por si mismos. Es decir, la operación sub_bytes realmente no hace nada ¡Esa es la vulnerabilidad! En cada ronda, solo se desordena el estado $S$ y se le hace XOR con una clave de ronda $K_i$ desconocida.

Reordenar el estado $S$, es fácil utilizando las operaciones inversas: inv_shift_rows e inv_mix_columns gracias a que, como ya se dijo, estas operaciones no dependen de la clave. Solo nos queda revertir el XOR y para eso parece que necesitamos las claves $K_i$. Pero si lo analizamos byte por byte y no como bloque, notaremos que cada byte de $S$ se hace XOR con 10 valores desconocidos (uno por cada clave de ronda). Podemos mentalmente agrupar esos 10 valores y hacerles XOR entre ellos para obtener un solo valor desconocido $k_r$. Ahora ya no necesitamos conocer cada clave de ronda independientemente, nos basta con obtener el $k_r$ para cada byte del estado.

$S_{i,j} \oplus k_0 \oplus k_1 \oplus … \oplus k_n = S_{i,j} \oplus (k_0 \oplus k_1 \oplus … \oplus k_n) = S_{i,j} \oplus k_r$

En resumen, todo el cifrado se ha resumido en un XOR de la forma:

$Ciphertext = Plaintext \oplus Key$

Gracias a que tenemos un archivo cifrado del cual conocemos el texto plano, podemos realizar un ataque de texto plano conocido y recuperar la clave.

$Key = Plaintext \oplus Ciphertext$

Y luego usar esa clave para descifrar los demás bloques:

$Plaintext = Ciphertext \oplus Key$

Solución

Aprovechamos que en el archivo aes.py ya están definidas las operaciones que necesitamos y al final agregamos este código.

def xorea(a, b):
    return bytes([x^y for x,y in zip(a,b)])


with open('testcipher.txt', 'rb') as fd:
    ciphertext = fd.read(16)

state = bytes2matrix(ciphertext)
inv_shift_rows(state)
for i in range(9):
    inv_mix_columns(state)
    inv_shift_rows(state)
ciphertext = matrix2bytes(state)
known_plaintext = b'testingaes123456'
xor_key = xorea(ciphertext, known_plaintext)

print('XOR KEY: {}'.format(xor_key))

with open('cipher.txt', 'rb') as fd:
    ciphertext = fd.read()

flag = b''
for block in [ciphertext[i:i+16] for i in range(0, len(ciphertext), 16)]:
    state = bytes2matrix(block)
    inv_shift_rows(state)
    for i in range(9):
        inv_mix_columns(state)
        inv_shift_rows(state)

    block = matrix2bytes(state)
    flag += xorea(block, xor_key)

print('FLAG: {}'.format(flag))

$ python aes.py
XOR KEY: b'\xb2\xa9Y),\xd3\xd43\xf8tv\x8a\xf6\xe0\xfe\xa8'
FLAG: b'ONA{7cb93a946dae527c44fa794956d948d0586137a3b99cd80df029bc95435f5a97}\x0b\x0b\x0b\x0b\x0b\x0b\x0b\x0b\x0b\x0b\x0b'

Flag: EKO{7cb93a946dae527c44fa794956d948d0586137a3b99cd80df029bc95435f5a97}